Transition Gradient from Standing to Traveling Waves for Energy-Efficient Slope Climbing of a Gecko-Inspired Robot
Worasuchad Haomachai
Zhendong Dai
Poramate Manoonpong
Nanjing University of Aeronautics and Astronautics, Nanjing, China
Vidyasirimedhi Institute of Science & Technology, Rayong, Thailand
Abstract
Lateral undulation patterns of a flexible spine, including standing waves, traveling waves, and their transitions, enable agile and versatile locomotion in sprawling animals. Inspired by this, we proposed body-wave transition strategies for energy-efficient inclined-surface climbing of a gecko-inspired robot with a bendable body. Using the robot as a scientific tool, we searched a large space of body movements (i.e., percentage of traveling waves and stride frequency) to explore climbing performance at different slope angles. Consequently, we designed a body-wave strategy to smoothly transition from a standing wave at low speeds to a traveling wave at high speeds to achieve energy-efficient climbing for each slope angle. Through a real robot experiment on the steepest slope (30 degrees), we demonstrated that the robot can reduce energy consumption by 7% compared to climbing with a constant body movement owing to the transition gradient from standing to traveling waves with an optimal speed. To this end, our study can pave the way for the development of climbing robots that utilize multiple body movement patterns with smooth transitions. Moreover, it can make a valuable contribution to biologists by formulating a novel hypothesis concerning the energy efficiency of gecko climbing.
Simulated Robot Climbing Experiments
Physical Robot Climbing Experiments
Analyzing a stride length, involving energy efficiency, using a geometrical model
CoT is influenced by two factors for this study, which consist of energy consumption and the traveled distance. For traveled distance, we use a simple geometrical model to estimate the stride length of the robot (FIG_WEB1). In this model, we assume that stride lengths are constant without any slippage during locomotion, and the movements of the left and right legs are symmetrical. Therefore, we can calculate the stride length (
) based on the assumption as follows:
is the leg length (i.e., 16.49 cm for our robot) which is set to a constant value. 
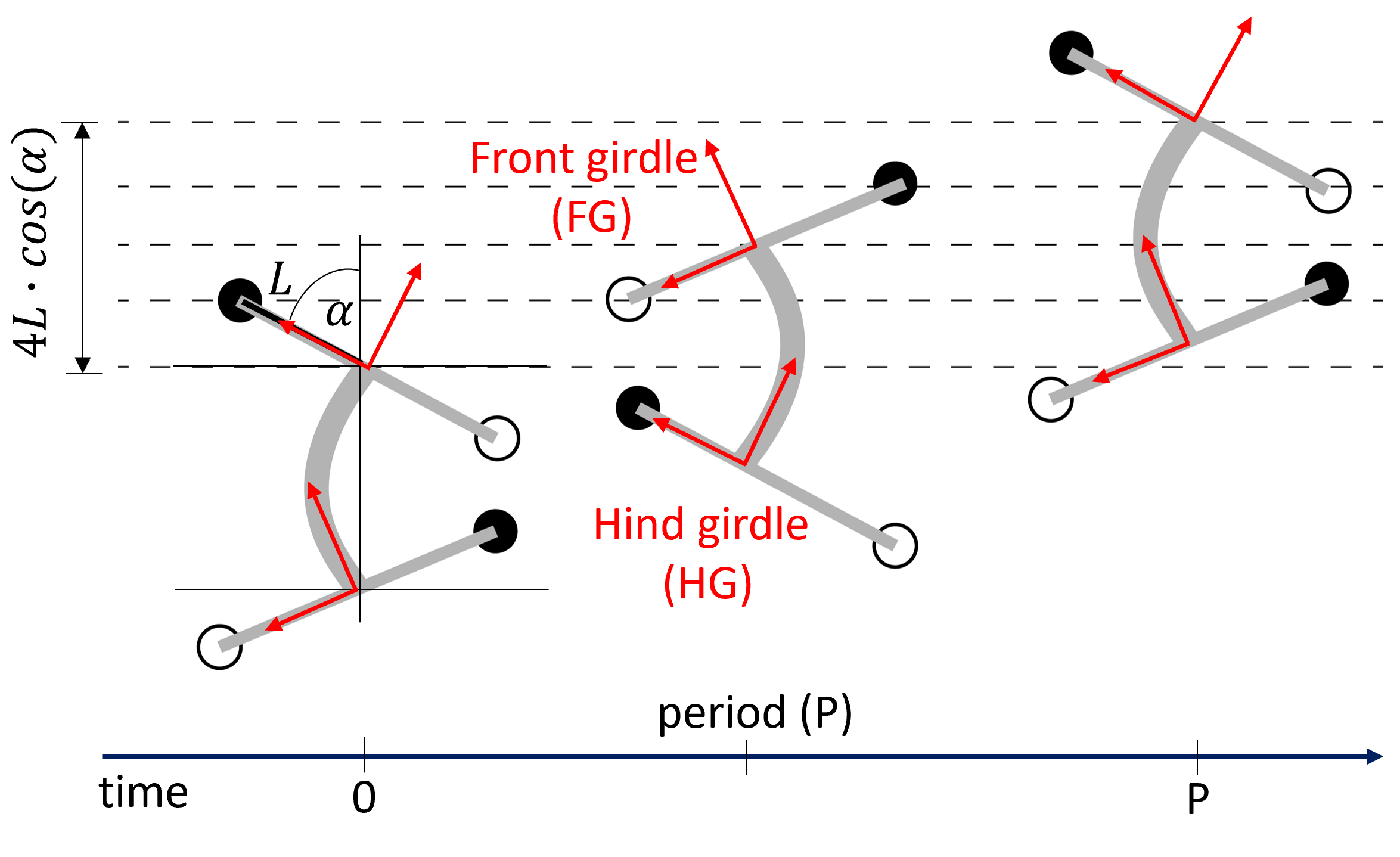
Setting the front girdle frame as the body’s base (
, 
) allows us to calculate the position of the hind girdle frame (
, 
) through the body’s forward kinematics (FIG_WEB2). This can be achieved by solving the following equation:
where each segment length of our robot body is 
= 9 cm, 
= 7.5 cm, 
= 7.5 cm, and 
= 9 cm. Each angle of rotation of body joints 1, 2, and 3 is defined as 
, 
and 
, respectively. It is important to note that motor signals from the CPG-based neural controller drive the body joint angles.
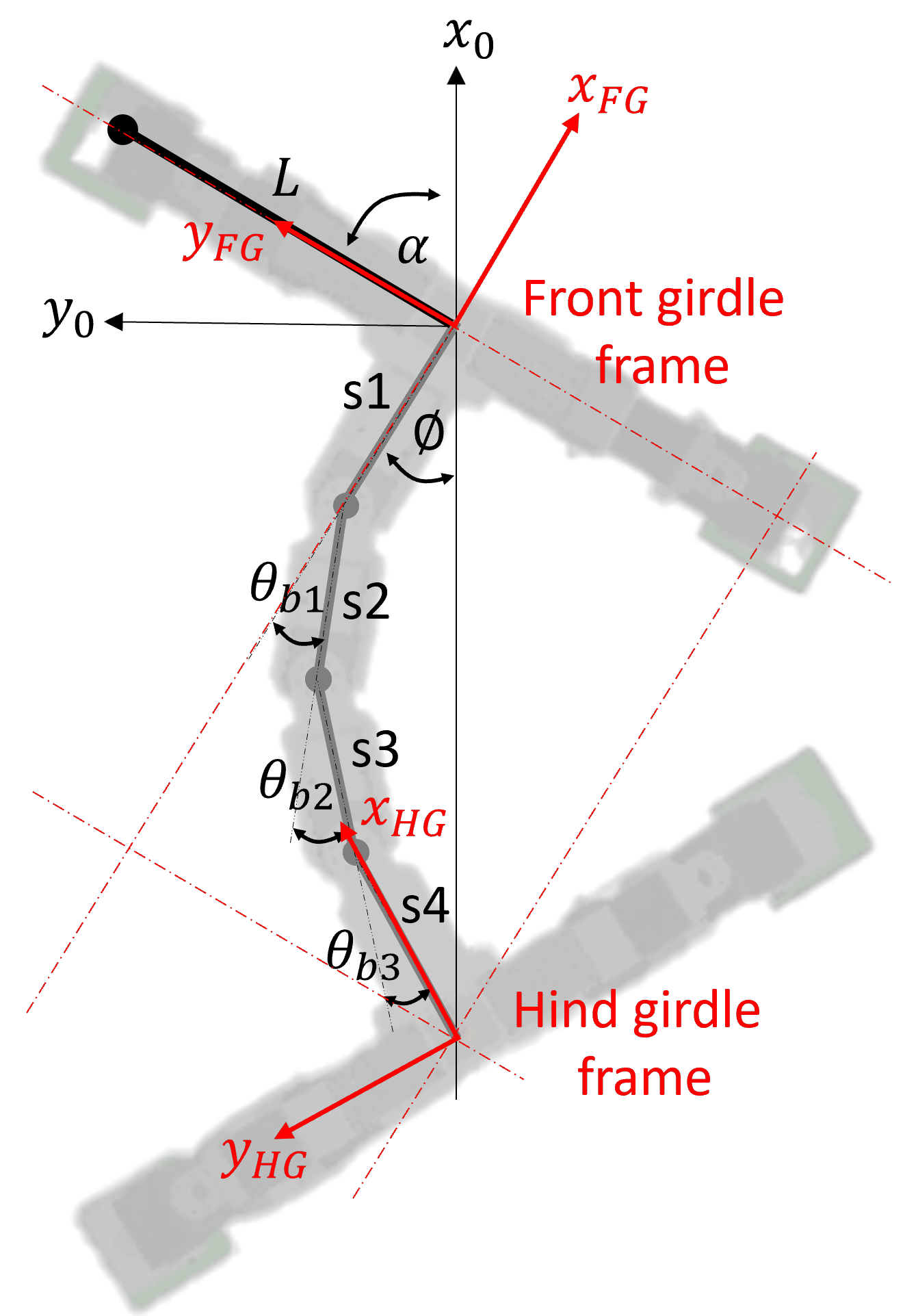
At the beginning of the stance phase, we assume that the forward direction of locomotion (i.e., x-axis of the world frame (
) is aligned with the line passing through both girdles (see FIG_WEB2). Note that and 
represent the coordinates of the world frame. Therefore, we can calculate the angle of 
at the beginning of each stride as follows:
Where is the angle of the position of the hide girdle frame (, ) related to the front girdle frame (the body’s base frame). With the assumption that both girdles are aligned on the x-axis of the world frame (), this can be interpreted as the angle between the x-axis of the world () and the body’s base frame or (see FIG_WEB2).
Based on the geometric relationship of the model, we obtain the angle of 
for calculating the stride length ().
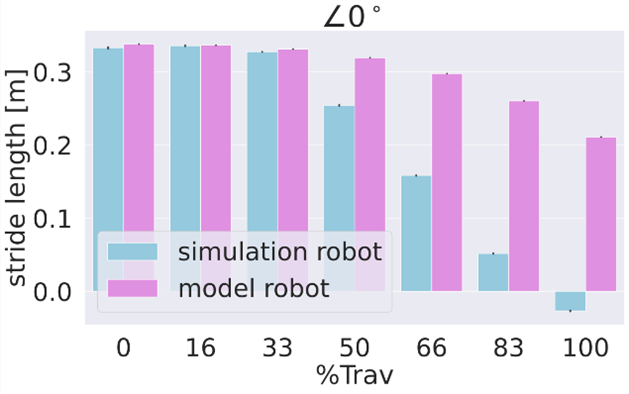
By using this robot’s geometrical model, which is driven by the motor control signals from the neural control, the stride length of each body pattern is obtained as shown in FIG_WEB3. To verify the accuracy of the geometrical model, we compared the stride length results of the model with those obtained from our simulation robot for each body pattern. The difference is referred to as the model error.
At 0%, 16%, and 33 %Trav, the geometrical model and simulation robot exhibit nearly identical stride lengths, indicating small model errors. However, at 50%, 66%, 83%, and 100 %Trav, there is a significant difference between the geometrical model and simulation robot, reflecting large model errors (FIG_WEB3).
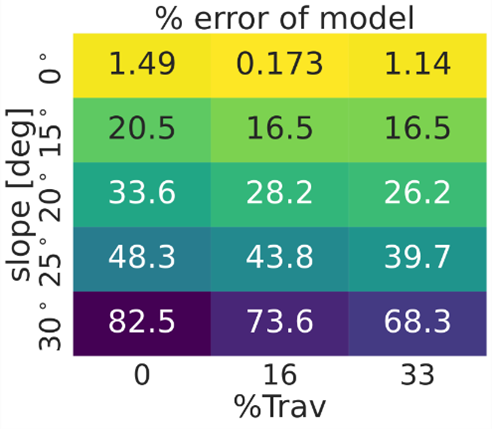
According to the small model errors of 0%, 16%, and 33 %Trav at a 0-degree angle, we further investigate higher inclined slopes, including 15, 20, 25, and 30-degree angles. The result of comparing the stride length of the model and simulation robot is shown in FIG_WEB4. The percentage error of the model is greater than 15% when climbing on a slope.
To answer the question “Can the model be verified by the experimental results?” we would answer “yes” but only on moving a level floor (0 deg). The geometrical model can estimate the stride length of robot locomotion, which can be verified by the experimental results at a 0-degree angle and at certain body-wave patterns (i.e., between 0% and 33 %Trav).
In addition, the stride lengths from the model estimation are 0.3379 m, 0.3363 m, and 0.3312 m for 0%, 16%, and 33 %Trav, respectively. If we assume that all body patterns have the same mass and almost the same energy usage, the most energy efficient locomotion obtained from the model is 0 %Trav since the model at 0 %Trav can achieve the longest stride length. According to this, the answer to the question “Can the CoT be estimated by the model?” would be “no” for this geometrical model because 0 %Trav is not the most energy-efficient locomotion from our experimental result (see in Fig. 3A). The most energy-efficient locomotion from our experiment at 0 deg is 16 %Trav.
The delay line mechanism
The body wave pattern is generated by using delay line units to shift the phase of the CPG signal (i.e., the output of CPG neuron 1 (
)) to obtain three different signals for driving three body joints. A delay line’s function is to add a time delay between its input and output, as shown by the equation below:
where 
the input signal (here the CPG signal). 
is the time step index (=0,1,2,…). 
is the delay factor. 
is the delayed output signal for motor control.
For our neural control network (Fig. 2A), there are three delay lines (
,
,
) for driving three body joints (b1,b2,b3). All of them receive the same input signal, which is the output of CPG neuron 1 (). We empirically adjusted the delay factors (,,) in the delay lines to determine the proper phase shifts of the output signals that control the body joints (b1,b2,b3), aiming to achieve body wave patterns or traveling waves.
For example, 50 %Trav (or 50% traveling wave) means that the phase of the second body joint b2 is shifted from the first body joint b1 by π/3 radians, and the phase of the third body joint b3 is shifted from b2 by π/12 radians or from b1 by π/3 + π/12= 5π/12 radians. To generate this body-wave pattern, we apply different delay factors to the CPG signal () as follows:
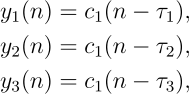
where 
, 
and 
are applied to control b1, b2, and b3, respectively. is set to zero (i.e., the output signal is the same as the CPG signal without any phase shifting). is set to 20 to shift the phase of b2 from b1 by π/3 radians. is set to 25 to shift the phase of b3 from b2 by π/12 radians or b1 by π/3 + π/12= 5π/12 radians. In our setup, the phase shift can vary from 0 to 2π by adjusting from 0 to 120.
According to the above mechanism, our control network with delay lines can generate various body wave patterns by setting the delay factors (
).
The transition gradient of body movement is performed by simultaneously changing body patterns (%Trav) through the delay factors (,,) and stride frequency through the extrinsic modulatory input (MI) of the CPG model changing body patterns during the first three strides and subsequently maintaining the patterns after the third stride. The following rules are applied:
(i) 1st stride: select a state with a minimum average of CoT.
(ii) 2nd and 3rd strides: change to a neighboring state in the minimum CoT region that exhibits the maximum velocity.
For more understanding, we used a state to represent body movement parameters which consist of percentage of traveling waves (%Trav) and stride frequency when the robot climbs at different slope angles. For example, 
indicates that the robot climbs at 30 degrees and during the 1st stride the robot performs 16% of traveling waves (=0, =6, =8) with a stride frequency of 0.33 Hz (MI=0.18).
More specifically, we demonstrated a body-wave transition strategy at a 30-degree slope angle from the first to third stride step-by-step (Fig. 3B):
1st stride: the robot begins climbing at 30 degrees with a %Trav of 16% and stride frequency of 0.33Hz. At the moment, the speed of the robot is 0.048 m/s and CoT is lowest value (0.28). The blue circle indicates the selected state , and the blue transparent arrow represent the state transition.
2nd stride: the robot performs the next state 
. By performing the first two strides, the robot consumes 0.20 of CoT and its speed is 0.066 m/s.
3rd stride: the robot proceeds to the steady state 
. By performing the first three strides, the robot speed is 0.085 m/s and CoT = 0.16.
Therefore, the gradient transition for climbing at 30 degrees can be generated as a series of state: , , and from the first, second and third strides, respectively. Furthermore, the gradient transition strategy of a 30-degree slope angle is applied to a real robot with its body joint signals illustrated in Fig. 5C.
Analyzing the friction in the motors and adhesion surface, involving control strateties
To address this issue, we conducted new experiments to investigate the impact of friction on the motors and adhesion surfaces. We implemented a pair of extension springs beside each body motor/joint (see Mark-II, Fig 5A). Each extension spring, with a stiffness of 140 N/m, simulates additional motor resistance or friction. In principle, this modification increases the difficulty in tracking the motor signal or the desired body-wave pattern, implying higher motor resistance or friction. Additionally, we covered the robot feet with silicone rubber Dragon Skin 30 to increase adhesion to the acrylic surface. The friction coefficient between the silicone rubber foot and acrylic is 0.87, exceeding that of the original EPDM rubber foot, which has a friction coefficient of 0.58 (Mark-I, Fig. 5A).
At a slope angle of 30 degrees, the new results from the Mark-II robot, equipped with springs and silicone feet, demonstrate that employing a body-wave transition strategy results in an average CoT of 59.2 at a velocity of 0.0345 m/s, whereas a constant body-wave movement consumes an average CoT of 63.1 at a velocity of 0.0320 m/s. The energy consumption of the body-wave transition strategy was reduced by approximately 6.5%, compared to the constant body-wave movement, owning to the transition gradient of body movement.
When comparing the performance of the Mark-I and Mark-II robots, we observed that Mark-II exhibited higher CoT than Mark-I in both body-wave transition and constant body-wave conditions. This is due to the fact that the body motors of Mark-II require more current to operate and compensate for motor resistance/friction induced by the installed springs. Furthermore, the highly adhesive silicone feet of Mark-II present a challenge with the used simple leg trajectory, as it might not be able to ensure sufficient ground clearance during the swing phase. If a foot touches the ground during the swing phase, the strong adhesion of the silicone foot creates resistance, preventing forward motion. In contrast, the standard rubber foot allows for slip during undesired ground contact in the swing phase without significantly disrupting forward motion. It is important to note that the center of mass (COM) of the robot shifts towards the rear when climbing on a slope, leading to a challenge in maintaining sufficient ground clearance for the hind feet.
Taken together, the friction in the motors and adhesion surface can have an impact on climbing performance in general. Nevertheless, these two factors do not affect our experimental results and control strategy, as both robot versions (Mark-I and Mark-II) consistently demonstrate that a body-wave transition strategy is more energy-efficient than a constant body-wave movement.
Citation:
@article{haomachai2024transition,
title={Transition Gradient from Standing to Traveling Waves for Energy-Efficient Slope Climbing of a Gecko-Inspired Robot},
author={Haomachai, Worasuchad and Dai, Zhendong and Manoonpong, Poramate},
journal={IEEE Robotics and Automation Letters},
year={2024},
publisher={IEEE}
} If you have any questions or doubts about this project, you are welcome to contact me. My email address is haomachai@gmail.com